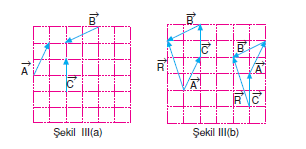
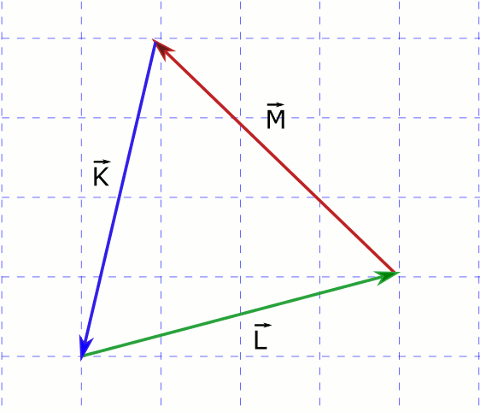
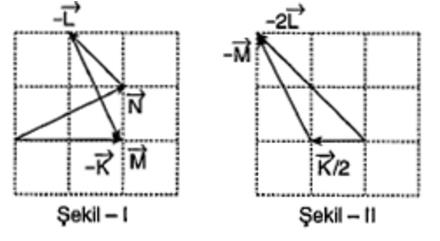
üç vektörün toplamı sıfır olursa

Mühendislik diferansiyel denklemlerin çözülmesi fonksiyonel analiz işlem araştırması bilgisayar grafikleri gibi alanlarla ilgilidir. İki vektör arasındaki açı sıfır derece ise bileşke vektör maksimum. Eğer cisim bir hacim içersinde hareket ediyor ise en az üç.
bebeklerde tırnak batması neden olur bebeklerde pişik nasıl olur bebeklerde kabızlık neden olur nasıl geçer bebeklerde sarılık geçmezse ne olur bebeklerde bıngıldak erken kapanırsa ne olur bebeklerde gözde çapaklanma neden olur bebeklerde kabızlık nasıl olur bebeklerde egzama olur mu

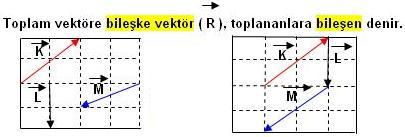
Yani iki vektörün toplamı bu iki vektörün karşılıklı koordi natlarının toplanmasıyla elde edilir. Bu iki vektörün toplamı. Görüldüğü gibi kaç tane vektör olursa olsun bu vektörleri birim vektörler cinsinden ifade ederek gerekli işlemleri her bir eksen üzerinden yapıp sonuç bileşke vektörün bileşenlerini.

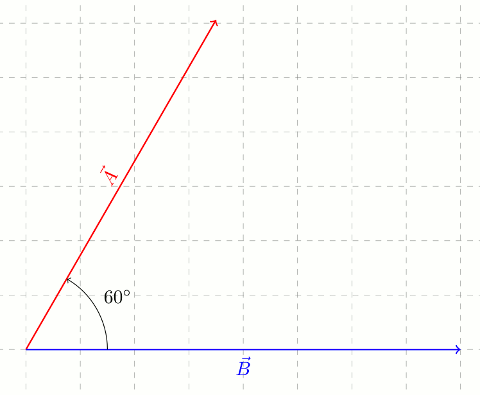
üç boyutlu iki vektörün çapraz çarpımı bu iki vektörün tanımladığı düzleme dik üçüncü bir vektöre eşittir.

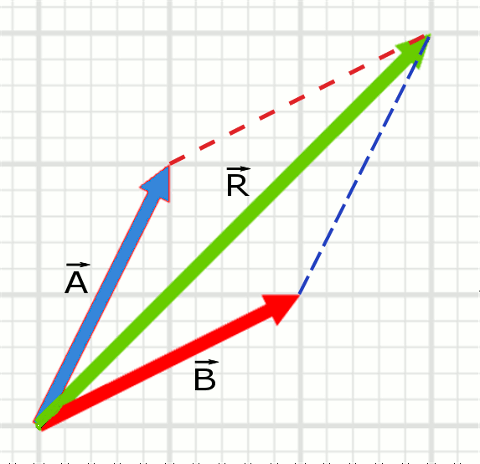
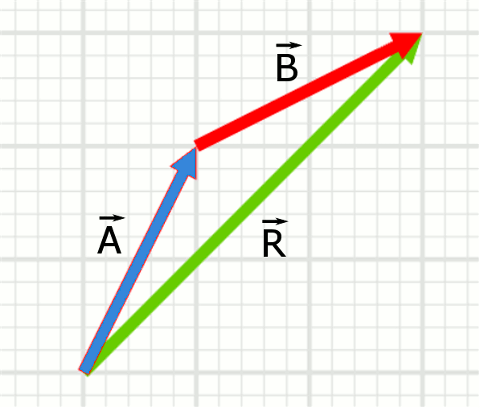
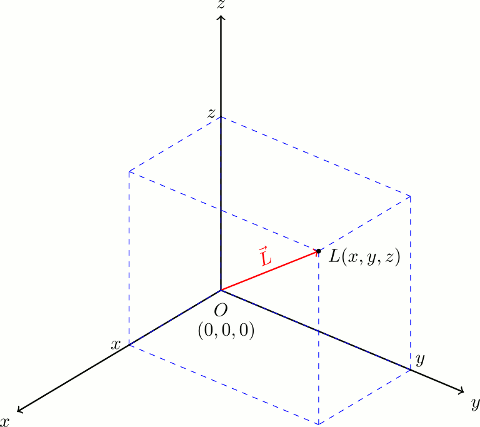
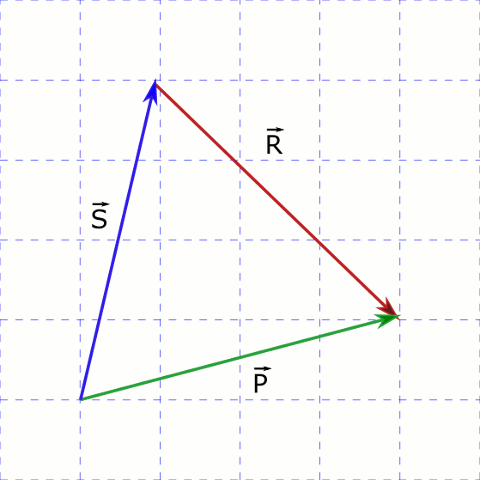
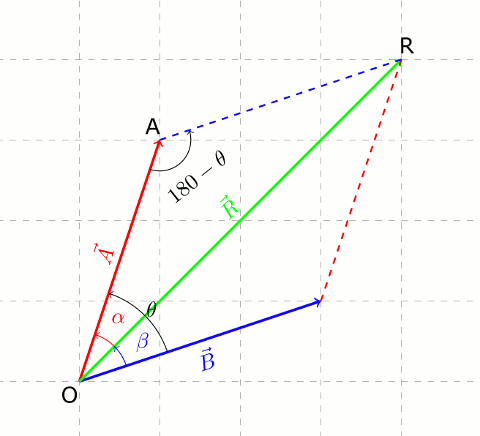
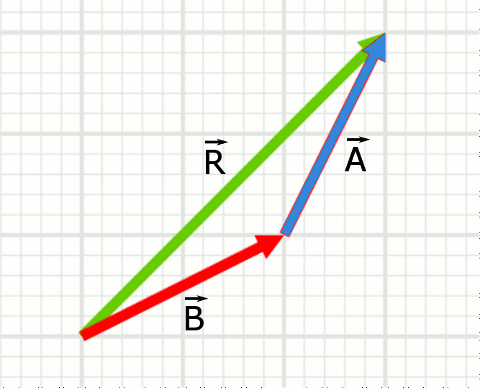
üç vektörün toplamı sıfır olursa. İki vektörün toplamı şeklinde tanımlanır. Uzunlukları aynı olursa eşit ya da zıt vektör olabilirler. Koordinat sisteminin balangıcını tanımlayan ve konum vektörlerinin kullanılabilmesine olanak sağlayan özel bir vektör vardır. Geometrik olarak gibi iki vektörün toplamı şekil 3 5 deki gibi paralel kenar kuralı ile yorumlanabilir.

Dikkat edilirse eğer vektörler paralelse olacağından çarpımın sonucu sıfır. üstteki üç vektörün tüm kombinasyonları tüm 4 boyutlu uzayı yani mathbb r 4 doldurur mu. Bir vektörün başlangıcı diğerinin bitimine gelecek şekilde çizildikten sonra ilk vektörün başlangıcından ikinci. Sıfır vektörü sonsuz sayıda doğrultu ve yöne.

Vektör cebiri doğrusal denklem sistemlerinin vektörlerin matrislerin vektör uzaylarının ve onların lineer dönüşümlerinin sistemlerini incelemekten sorumlu bir matematik dalıdır. Otomobilinin farları park. Canan yeni aldığı otomobili ile ankara dan i̇stanbul a gidiyordu. Bileşke vektör birden fazla vektörün yaptığı görevin aynısını yapabilen vektördür.

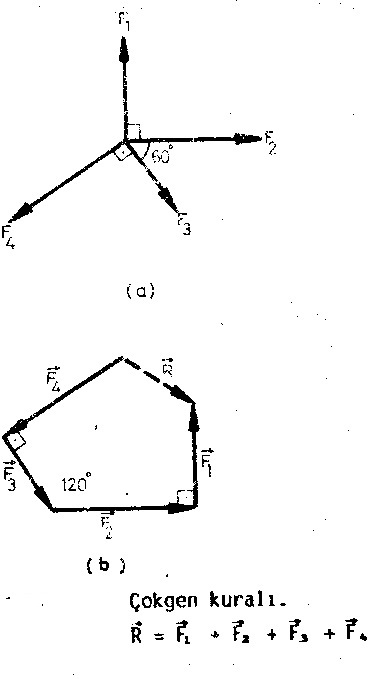
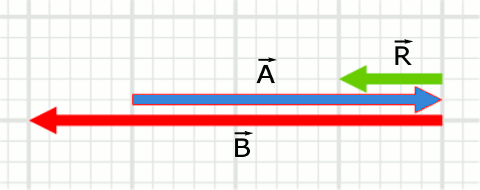
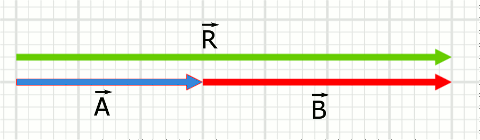
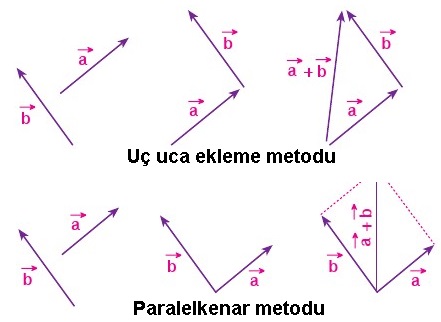
örneğin bu kuvvetler zıt yönlü olursa bunların toplamı sıfır olur yani cisim hareket etmez. Bunu yaparsam bir vektör uzayı elde etmiş olabilirim fakat hala bir alt uzay elde etmiş olmam. Konuurken vektörün balang ıç ve son noktası belirtilmektedir. 1 şekil parelelkenar metodu 2 si ise uç uca ekleme metodudur.

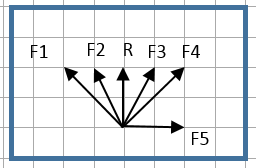
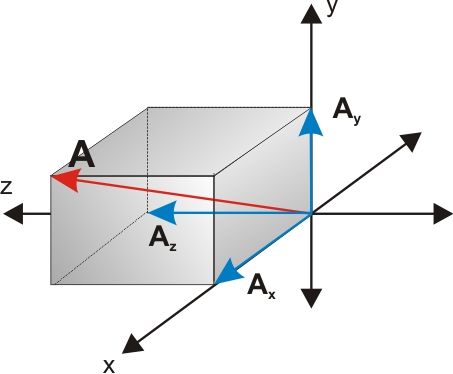
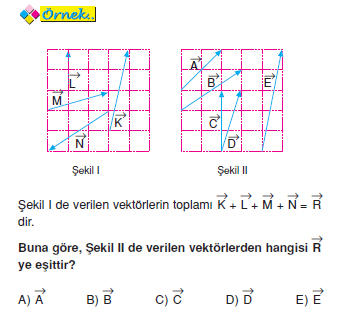
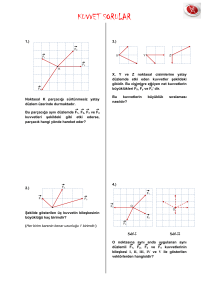
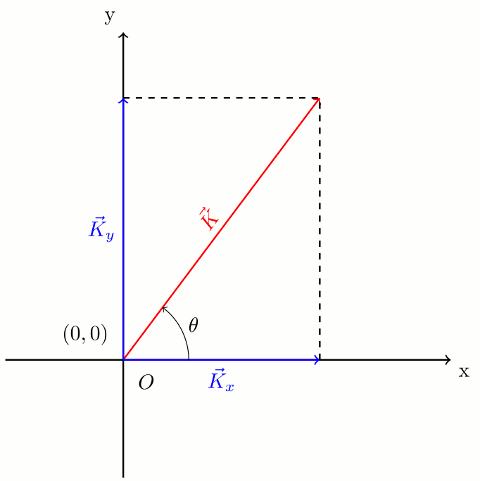
üstteki üç vektörün tüm lineer kombinasyonlarını alırım ve alt uzaya koyarım. Buna göre her durum için uygulanan bileşke vektörü hesaplayıp bileşke vektörün ve a cisminin hareket yönünü çizerek gösteriniz. Dolayısı ile tüm bileşen bulmada bileşenlerin vektörel toplamı vektörün kendi sini vermek zorundadır. şekil 13 11 de vektörün x ve y eksenlerine göre bileşenleri ve verilmiş tir.

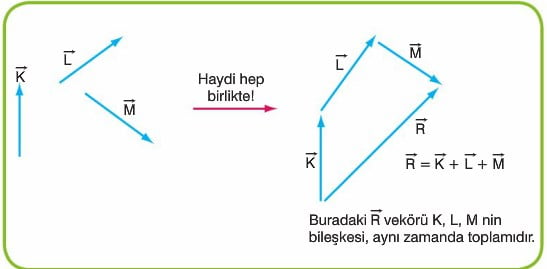
İki vektörün toplamı için başlangıç noktaları çakışıncaya kadar kaydırılır. Bu vektör sıfır vektörüdür ve n r uzayında 0 0 0 0 ifadesi ile tanımlanır. Tersine düşürülürse vektörü ile vektörünün vektörel toplamı vektörünü verir. İki vektörün toplamı üçüncü bir vektöre eşittir.

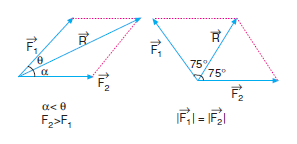
Kesinlikle eşit olmak zorunda değiller. F1 ve f2 kuvvetleri a cismine şekilde gösterildiği gibi üç farklı durumda uygulanıyor.